The base of a numeric system is the total number of digits used in that system. In everyday life, we use the decimal number system, which has ten digits 0-9. The Binary number system, which has only two digits, is used in computers.
This might make you wonder why that is the case. Why are computers not programmed to use the decimal number system instead? I am writing this article to clarify the process for you.
As a technology geek, I have always been interested in computers, and the way computers use the binary number system to simplify their tasks has always fascinated me. I will break it down for you in this article.
So keep reading this article until the end to learn why computers use binary.
What is the Binary Number System?
In mathematics, the binary number system is a positional numeral system that uses 2 as its base and only needs the two symbols 0 and 1 for its digits, as opposed to the typical 10 symbols required by the decimal system. Each digit in a binary number is called a bit.
The use of binary numerals is widespread in computer programs. The binary digits 0 and 1 are used in all computer coding and languages, including C, C++, Java, etc., to build programs and encode digital data. Only the coded language is understandable to the computer.
As a result, a set of facts or information is represented by this 2-digit number system as discrete bits of information.
Arithmetic operations in the binary number system are a bit different than how you are used to them in the decimal number system. For example, 1+1=2 in the decimal number system. But, 1+1=10 in the binary number system.
The binary number has only two digits. So, after 1, there is no 2. You move on to several 2 digits just like you would for 9, which is the final digit in the decimal number system.
You can add, subtract, multiply, and divide a binary number with another. Binary numbers are also helpful in advanced mathematics to prove certain theorems. For example, you can use binary to prove certain theorems about cantor sets.
Related contents you should read about why are Dell computers so expensive?
Why Are Binary Numbers Used in Computer Programming?
You do not need much-advanced mathematics knowledge to understand computer programming. Binary numbers are straightforward to understand. As binary numbers only have 2 digits, everything can appear to be more simplified.
Computers are not as good at understanding words or numbers as people are. The end user can ignore this with modern software. Still, at the most basic levels of your computer, everything is represented by binary electric signals that register in one of two states, on or off.
Because binary is the most straightforward counting system currently in use, computers utilize it to code everything from memory to HD video streaming. A computer can quickly process millions of inputs thanks to binary.
Here are the reasons why computers use binary:
1. Electrical Signals Have 2 States
Transistors, or tiny electrical switches, are used by computers as communication devices. A computer can easily comprehend a switch.
The switch can be activated to the on position by the electrical current or remain in the off state. Because there are only two possibilities in binary, on and off, the computer can easily comprehend it.
Since each placeholder in a base-10 system has 10 potential values, it is significantly more difficult.
Two binary values should represent electrical signals: 0 for low and 1 for high voltage. Consider a machine that the computer may represent in two states: off (value 0) and on (value 1). The computer can quickly process this information.
Instead of an unlimited range of continuous voltage values, this broad generalization condenses the range of interpretation of each electric signal into 2 distinct values.
We may build coded systems based on binary bits to assist in our computational duties once we have this approach to operating and interpreting electronic circuits.
Some examples of these systems include binary logic (limited to two possible values), base-2 number representation of numerical values, or other methods that rely on a series of binary numbers to represent text, images, or sounds.
Also read about can i use a FreeSync monitor with an Nvidia card?
2. Boolean Logic
Computer programs execute commands using a fairly specific logic scheme. Boolean logic is the term for this. Three simple words known as the Boolean Operators—Or, And, and Not—are the foundation of the algebraic concept known as boolean logic.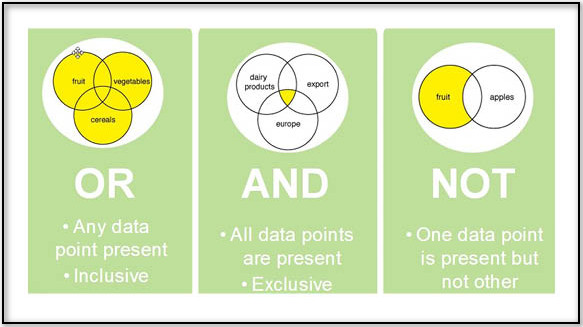
The main principle of Boolean logic is that all values can either be true or false.
The Boolean operator OR indicates that a specified query’s value is true if any of a set of two or more conditions is satisfied.
The Boolean operator AND indicates that a specified query’s value is true if all of a set of two or more conditions is satisfied.
The Boolean operator NOT is used to exclude certain conditions from the query. If the NOT operator prepends a logical variable, it means the logical value of the logical variable will be considered false.
A data type called boolean exists in all programming languages and can only store “true” or “false,” or, more specifically, 1 or 0.
The basic building blocks of conditional and control statements in programming languages are boolean variables and logical operators. Their significance cannot be underestimated.
Besides that, several other inventive and complex ways to use binary integers in programming languages exist. The program is easy to understand for the computer because of binary numbers, and it can take action quicker.
3. Text and Character Representation in Binary
Computers can represent text and characters by using the binary number system. ASCII (American Standard Code for Information Interchange) and Unicode are the two most widely used character representation systems (an ASCII extension).
These systems give each character a distinct numeric value and store it in binary form. This method works well to represent characters and symbols in English and specific European languages, but it is woefully insufficient to represent characters and symbols in other languages.
Unicode was created to support more symbols. Unlike ASCII’s initial use of 7 bits for each sign, Unicode initially employed 21 bits. The range of values that can be utilized to represent characters is significantly increased.
The Unicode system allows for the use of the original ASCII codes. The most widely used encoding system in online applications is UTF-8, a Unicode-based system. The UTF-8 can represent an even greater range of characters because it can use up to 32 bits per symbol.
4. Numerical Representation
You can easily convert any decimal number to binary and any binary number to decimal. A binary number can be converted to a decimal by multiplying digits by powers of 2. The power is increasing from right to left.
A decimal can be converted to a binary number by continuously dividing by 2, where the quotient replaces the dividend on the next step. We take the remainders in reverse to get the equivalent binary form.
Here is an algorithm to convert a binary number to an equivalent decimal number:
- Input: number in the binary system as variable named num.
- Set base=0 and deci=0
- While num>=10,
Divide num by 10 and store the quotient as the new value of num and the remainder as rem.
Set deci=2^base*rem+deci
Set base=base+1
- Output: deci
The output is the equivalent number in the decimal system.
Similarly, an algorithm to convert a decimal number to an equivalent binary number is also easy.
Here is an algorithm to convert a decimal number to an equivalent binary number:
- Input: number in the binary system as variable named num.
- Set base=0 and bin=0
- While num>=2,
Divide num by 2 and store the quotient as the new value of num and the remainder as rem.
Set bin=10^base*rem+bin
Set base=base+1
- Output: bin
The output is the equivalent number in the binary system.
So using binary numbers, we can easily represent every decimal number as conversion between the numbers is pretty simple.
5. Image Representation
Numbers are frequently used to represent visuals. The most frequent way that images are created in computers is with tiny colored squares known as pixels.
The images on our screens are composed of millions of little, colorful squares. There are other ways to code colors in pixels, but RGB coding is the most popular one (Red, Green, Blue).
Red, green, and blue hues are combined in RGB coding to create all the color shades we see in contemporary electronics. An integer between 0 and 255 codifies the three color components.
As you can express numbers in binary systems, you can also define pixels. An image is a combination of many pixels. Therefore, you can represent images using binary numbers.
6. Sound Representation
Since sound waves are analog, they must be transformed into binary before being processed by a computer. To store the waveform digitally, the computer must first convert the waveform into a numerical representation.
An Analogue-to-Digital Converter is what we employ for this (ADC). An ADC functions by periodically sampling the sound wave. Both sample rate and bit rate impact the file’s quality and size.
The number of samples taken each second is referred to as the sample rate, and the higher the sampling frequency, the better the sound quality.
The bit rate describes how many bits are used to store each sample, and the more bits sampled, the more accurate the file is while simultaneously increasing file size.
So, as you can see, binary numbers allow computers to efficiently represent different forms of data. This is why computers use this number system.
Also, check out our separate post on can i use two different brands of RAM?
FAQ
What is a byte?
A bit(a binary digit) is the smallest piece of data that a computer can process and store. A byte is an eight-bit sequence that is regarded as a single entity.
Do smartphones use binary numbers?
Yes, smartphones communicate via binary numbers. To maximize the amount of data that smartphones can transfer and the speed at which they can receive it, mobile devices convert the radio signal into a system of 1s and 0s, or binary.
Is there a universal binary code to represent text?
Yes, Unicode is the universal binary code to represent text.
Conclusion
Binary numbers make it easy to represent electrical signals. It is also easy to represent boolean logic. Binary numbers increase the speed of the processes.
Therefore, computers use binary numbers for good reasons. It can help make computing and other tasks much more straightforward. Using any other number system would complicate matters, making it difficult to program the computer.
If there is anything you did not understand, please comment below! I will try my best to assist you.
